The Impossibility of Distributed Consensus: Understanding the FLP Result

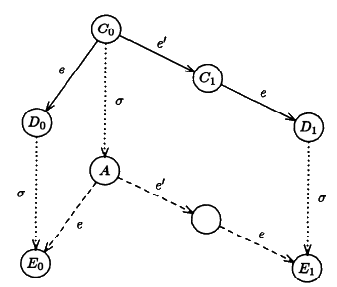
The FLP result explains why achieving consensus in an asynchronous system with even a single faulty process is impossible.

The Consensus Problem

The consensus problem involves a group of processes that must agree on a single binary value (0 or 1). This problem is crucial for various applications in distributed systems, such as database management and fault-tolerant computing. The challenge is to design a protocol that ensures all non-faulty processes eventually agree on the same value, despite the presence of faults.

Asynchronous Systems and Faults

The FLP result specifically considers asynchronous systems, where there are no guarantees about the timing of message delivery or the relative speeds of processes. This lack of timing guarantees makes the problem significantly more complex. Additionally, the paper assumes a reliable message system where messages are neither lost nor duplicated, but processes can fail by stopping (crashing) unexpectedly.

Key Concepts and Definitions

1. Bivalent and Univalent Configurations:

   • A configuration is the state of the system at a given point in time.
   • A configuration is bivalent if the system can still decide on either 0 or 1.
   • A configuration is univalent if the system is committed to a single decision value (either 0-valent or 1-valent).

2. Admissible Runs:

   • An admissible run is a sequence of steps (events) that the system can take, where at most one process is faulty, and all messages to non-faulty processes are eventually delivered.

3. Deciding Runs:

   • A deciding run is an admissible run where at least one process reaches a decision state.

The Impossibility Proof

The FLP result demonstrates that no consensus protocol can guarantee a decision in an asynchronous system with even one faulty process. The proof is constructed through a series of lemmas leading to a contradiction:

1. Existence of a Bivalent Initial Configuration:

   • The proof begins by showing that there must exist an initial configuration where the system is bivalent. This is crucial because it means the system's decision is not predetermined.

2. Bivalence Preservation:

   • The proof then shows that from any bivalent configuration, it is possible to reach another bivalent configuration without making a decision. This involves carefully constructing runs that avoid committing to a decision.

3. Construction of an Admissible Non-Deciding Run:

   • By repeatedly applying the above steps, the proof constructs an infinite admissible run where the system remains bivalent indefinitely, thus never reaching a decision.

Intuition Behind the Proof

The core intuition of the FLP result lies in the inherent uncertainty of asynchronous systems. Without synchronized clocks or reliable failure detection, processes cannot distinguish between a slow process and a crashed one. This uncertainty allows the construction of scenarios where the system can be kept in a state of indecision indefinitely.

Implications and Further Research

The FLP result has profound implications for distributed computing. It highlights the limitations of purely asynchronous systems and the need for additional assumptions or mechanisms (such as partial synchrony or failure detectors) to achieve consensus. Subsequent research has explored these avenues, leading to more robust consensus protocols under different models and assumptions.

Fischer, Lynch, and Paterson, in the FLP theorem proved the impossibility of consensus in an asynchronous system with one faulty process.

Key Terms

• FLP theorem: named after its authors Fischer, Lynch, and Paterson, states that in an asynchronous distributed system, it is impossible to achieve consensus if there is even a single faulty process. This means that no matter how the consensus protocol is designed, there will always be a scenario where the protocol cannot guarantee that all non-faulty processes will agree on a single value. This result highlights the fundamental limitations of fault tolerance in distributed systems without timing assumptions.

• Asynchronous System: A system where there are no guarantees about the timing of message delivery or the relative speeds of processes.

• Bivalent Configuration: A state of the system where the outcome of the consensus process is not yet determined and can still result in either of the possible decision values.

• Byzantine Fault: A type of fault where a component, such as a server, can fail and give conflicting information to different parts of the system.

• Consensus Problem: The challenge of getting a group of distributed processes to agree on a single data value.

• Distributed System: A network of independent computers that appears to its users as a single coherent system.

• Fault Tolerance: The ability of a system to continue operating properly in the event of the failure of some of its components.

• Impossibility Proof: A proof that demonstrates that a certain problem cannot be solved under specified conditions.

• Message Passing: A method of communication where processes or nodes send messages to each other to exchange information.

• Nonfaulty Process: A process that continues to operate correctly and does not fail during the execution of a protocol.

• Partial Synchrony: A model of distributed systems where the system is mostly asynchronous but has some bounds on message delivery times or process speeds.

• Quorum: A subset of nodes in a distributed system whose agreement is sufficient to make a decision.

• Replication: The process of sharing information across multiple nodes to ensure reliability and fault tolerance.

• Synchronous System: A system where there are known bounds on the time it takes for messages to be delivered and for processes to execute steps.

• Univalent Configuration: A state of the system where the outcome of the consensus process is already determined and can only result in one specific decision value.

• Vector Clock: A mechanism for capturing causality in distributed systems by associating a vector of counters with each event in the system.

• Window of Vulnerability: A period during which a system is susceptible to faults that can prevent it from reaching a consensus.

• Atomic Broadcast: A communication primitive where a message is sent to all nodes in such a way that if any node receives the message, all nodes receive it.

• Eventual Consistency: A consistency model used in distributed computing to achieve high availability, where updates to a distributed database will eventually propagate to all nodes.

• Leader Election: The process of designating a single process as the coordinator of some task distributed among several computers (nodes).

• Paxos: A family of protocols for solving consensus in a network of unreliable processors.

• Raft: A consensus algorithm designed to be understandable and used as an alternative to Paxos.

• CAP Theorem: A principle that states it is impossible for a distributed data store to simultaneously provide more than two out of the following three guarantees: Consistency, Availability, and Partition Tolerance.

• Distributed Ledger: A database that is consensually shared and synchronized across multiple sites, institutions, or geographies.

• Sharding: A database partitioning technique that divides large databases into smaller, more manageable pieces called shards.

• Gossip Protocol: A communication protocol used to spread information in a distributed system in a manner similar to the way gossip spreads in social networks.

@article{fischer1985impossibility,
	title={Impossibility of distributed consensus with one faulty process},
	author={Fischer, Michael J and Lynch, Nancy A and Paterson, Michael S},
	journal={Journal of the ACM (JACM)},
	volume={32},
	number={2},
	pages={374--382},
	year={1985},
	publisher={ACM New York, NY, USA}
}