The structure of an object can determine its size and indirection. Stack allocated objects can always be allocated on the heap manually (malloc or new) if needed. If the object has a pointer as a member, it is best to use new/delete vs malloc/free such that the constructor and destructor are called.
All experiments in this article are assumed to use the following headers and Print function:
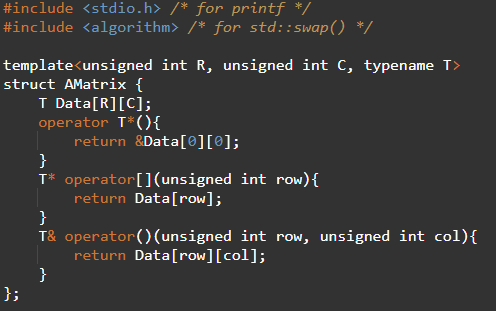
#include <stdio.h> /* for printf */
#include <algorithm> /* for std::swap() */
// A print method that shows how each element of a matrix can be printed
// just by incrementing the pointer
template<unsigned int R, unsigned int C, typename T>
void Print(T* ptr){
for (int r = 0; r < R; r++){
printf("\t");
for (int c = 0; c < C; c++){
printf("%d, ", *ptr);
ptr++;
}
printf("\n");
}
}
// An initialize method that assigns values to a matrix
// just by incrementing the pointer
template<unsigned int R, unsigned int C, typename T>
void Initialize(T* ptr){
for (int i = 0; i < R*C; i++){
*ptr = i;
ptr++;
}
}
Just like the Print function, let's assume a matrix has rows and columns - and is 0 index (0,0 is the first element of the matrix). Most define matrices as being row-oriented because row-reduction is a powerful procedure in matrix math. First, we define a matrix that manages its memory.
template<unsigned int R, unsigned int C, typename T>
struct MMatrix {
T* Data = NULL;
// The default constructor allocates the data
MMatrix() {
Data = (T*)malloc(sizeof(T)*R*C);
}
// The destructor de-allocates the data
~MMatrix() {
if (Data == NULL){return;}
free(Data);
Data = NULL;
}
// An operator to provide easy access to the data
operator T*(){
return Data;
}
// An operator to provide easy access to a row
T* operator[](unsigned int row){
return Data + row*C;
}
// An operator to provide easy access to an element
T& operator()(unsigned int row, unsigned int col){
return Data[row*C + col];
}
// Swapping rows is needed for row reduction
void Swap(unsigned int row1, unsigned int row2){
// use pointer math ... or ...
T* r1 = Data + row1*C;
// use this object api to get the pointer
T* r2 = this->operator[](row2);
for (int c = 0; c < C; c++){
T val = *r1;
*r1 = *r2;
*r2 = val;
r1++;
r2++;
}
}
};
This is a good start for a matrix. We can define it in terms of rows, columns, and type. Also, we'll never get a stack overflow error with this matrix because its Data is stored on the heap (malloc/free). This is nice unless the matrix is small... Then allocation and de-allocation seems like a waste.
Let's now try to keep everything allocated - while using the same basic API.
template<unsigned int R, unsigned int C, typename T>
struct AMatrix {
T Data[R][C];
// An operator to provide easy access to the data
operator T*(){
return &Data[0][0];
}
// An operator to provide easy access to a row
T* operator[](unsigned int row){
return Data[row];
}
// An operator to provide easy access to an element
T& operator()(unsigned int row, unsigned int col){
return Data[row][col];
}
// Swapping rows is needed for row reduction
void Swap(unsigned int row1, unsigned int row2){
std::swap(Data[row1], Data[row2]);
}
};
This matrix is purely stack allocated, and works the same way for new/delete as malloc/free - such we can define it on the heap to avoid stack overflow exceptions. One of the things we notice here is the array of arrays. We could give ourselves a little more power by defining operators for the row itself.
template<unsigned int C, typename T>
struct BMatrixData {
T Data[C];
operator T*(){
return &Data[0];
}
T& operator[](unsigned int index){
return Data[index];
}
BMatrixData<C, T> operator*(const BMatrixData<C, T>& other) const{
BMatrixData<C, T> ret;
for (int i = 0; i < C; i++){
ret.Data[i] = Data[i]*other.Data[i];
}
return ret;
}
BMatrixData<C, T> operator+(const BMatrixData<C, T>& other) const{
BMatrixData<C, T> ret;
for (int i = 0; i < C; i++){
ret.Data[i] = Data[i] + other.Data[i];
}
return ret;
}
BMatrixData<C, T> operator-(const BMatrixData<C, T>& other) const{
BMatrixData<C, T> ret;
for (int i = 0; i < C; i++){
ret.Data[i] = Data[i] - other.Data[i];
}
return ret;
}
BMatrixData<C, T> operator*(const T& val) const{
BMatrixData<C, T> ret;
for (int i = 0; i < C; i++){
ret.Data[i] = Data[i]*val;
}
return ret;
}
unsigned int Length() const {
return C;
}
};
template<unsigned int R, unsigned int C, typename T>
struct BMatrix {
BMatrixData<C, T> Data[R];
// An operator to provide easy access to the data
operator T*(){
return Data[0];
}
// An operator to provide easy access to a row
BMatrixData<C, T>& operator[](unsigned int row){
return Data[row];
}
// An operator to provide easy access to an element
T& operator()(unsigned int row, unsigned int col){
return Data[row][col];
}
// Swapping rows is needed for row reduction
void Swap(unsigned int row1, unsigned int row2){
std::swap(Data[row1], Data[row2]);
}
};
This matrix is also purely stack allocated, and works the same way for new/delete as malloc/free. It does not use an array of arrays, but instead uses an array of rows, which themselves are arrays. It does highlight the potential for row operations.
So let's see it. How does this perform? Here is the test of size, initialization, and swapping using stack semantics.
int main()
{
printf("sizeof(MMatrix<3,3, int>) = %d\n", sizeof(MMatrix<3,3, int>)); // 8
printf("sizeof(AMatrix<3,3, int>) = %d\n", sizeof(AMatrix<3,3, int>)); // 36
printf("sizeof(BMatrix<3,3, int>) = %d\n", sizeof(BMatrix<3,3, int>)); // 36
MMatrix<3,3, int> M;
AMatrix<3,3, int> A;
BMatrix<3,3, int> B;
printf("sizeof(M) = %d\n", sizeof(M)); // 8
printf("sizeof(A) = %d\n", sizeof(A)); // 36
printf("sizeof(B) = %d\n", sizeof(B)); // 36
Initialize<3,3,int>(M);
Initialize<3,3,int>(A);
Initialize<3,3,int>(B);
printf("M = [\n");
Print<3, 3, int>(M);
printf("]\n");
printf("A = [\n");
Print<3, 3, int>(A);
printf("]\n");
printf("B = [\n");
Print<3, 3, int>(B);
printf("]\n");
M.Swap(0, 1);
A.Swap(0, 1);
B.Swap(0, 1);
printf("\n\nAfter swap:\n");
printf("M = [\n");
Print<3, 3, int>(M);
printf("]\n");
printf("A = [\n");
Print<3, 3, int>(A);
printf("]\n");
printf("B = [\n");
Print<3, 3, int>(B);
printf("]\n");
return 0; // for success
}
So let's see the results:
sizeof(MMatrix<3,3, int>) = 8
sizeof(AMatrix<3,3, int>) = 36
sizeof(BMatrix<3,3, int>) = 36
sizeof(M) = 8
sizeof(A) = 36
sizeof(B) = 36
M = [
0, 1, 2,
3, 4, 5,
6, 7, 8,
]
A = [
0, 1, 2,
3, 4, 5,
6, 7, 8,
]
B = [
0, 1, 2,
3, 4, 5,
6, 7, 8,
]
After swap:
M = [
3, 4, 5,
0, 1, 2,
6, 7, 8,
]
A = [
3, 4, 5,
0, 1, 2,
6, 7, 8,
]
B = [
3, 4, 5,
0, 1, 2,
6, 7, 8,
]
All the matrix types allow for pointer access and take advantage of sequential memory. All the matrix types allow for both stack semantics. The swap API works for all matrix types.
What's next? You can try the example online.