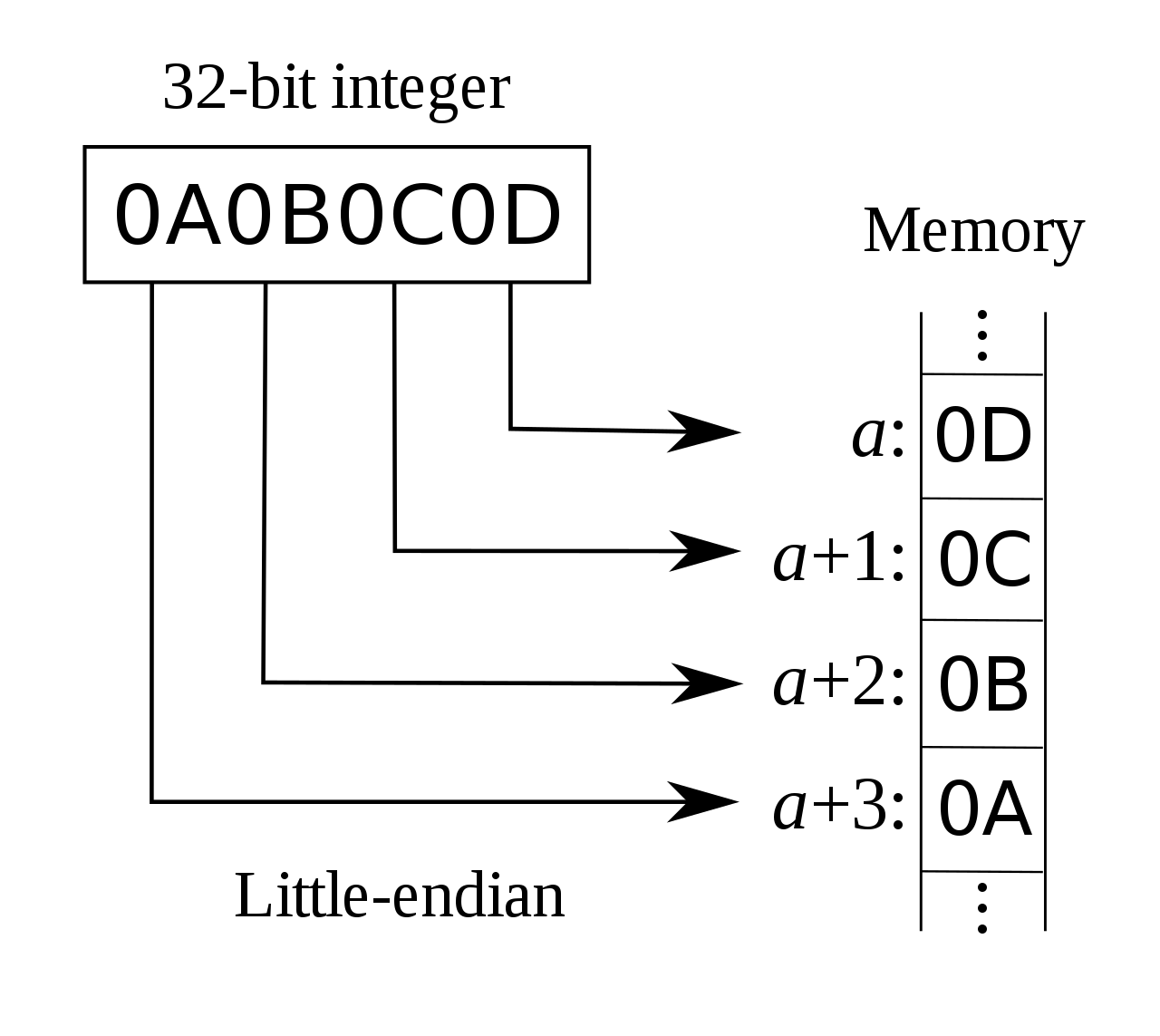
Endianness refers to the sequential order in which bytes are arranged into larger numerical values when stored in memory. Words may be represented in big-endian or little-endian format. Bits or bytes are ordered from the big end (most significant bit) or the little end (least significant bit). This often has to do with the processor architecture.
In C++ (as well as other languages), bit shifts can be used to set a power of 2.
For example, (1<<2) would be a 1 shifted 2 to the left, or 2^2 = 4.
This can be used to determine how the memory is laid out - or to inspect the value of any bit.
The bitwise & operator is used for comparison. For example 1 & 1 = 1 and 2 & 1 = 0.
This is because 01 & 01 = 01 and 10 & 01 = 00.
The bitwise | operator combines the two values such that 10 | 01 = 11.
Here is some code to test how items are stored in memory. We will use two arrays that are at the same memory address, but have different size elements.
int main()
{
// Define an array
unsigned int i[6]{0,1,2,4,8,16};
// Use these values to be the basis of an array of a different type.
unsigned long* l = (unsigned long*)i;
// Display the values of the first array
cout<<"sizeof(unsigned int)=" << sizeof(unsigned int) << "\n";
cout<<"i[0] = " << i[0] << "\n";
cout<<"i[1] = " << i[1] << "\n";
cout<<"i[2] = " << i[2] << "\n";
cout<<"i[3] = " << i[3] << "\n";
cout<<"i[4] = " << i[4] << "\n";
cout<<"i[5] = " << i[5] << "\n";
// Display the values of the second array.
cout<<"sizeof(unsigned long)=" << sizeof(unsigned long) << "\n";
cout<<"l[0] = " << l[0] << "\n";
cout<<"l[1] = " << l[1] << "\n";
cout<<"l[2] = " << l[2] << "\n";
// Now display the arrays in bitwise format
int ni = 5;
while (ni >= 0){
cout << "i[" << ni << "] = ";
int pi = sizeof(unsigned int)*8-1;
while (pi>=0){
if ((((unsigned int)1<<pi) & i[ni]) > 0){
cout << 1;
}
else {
cout << 0;
}
if (pi % 8 == 0){ cout << " ";}
pi--;
}
cout << "\n";
ni--;
}
cout << "\n";
int nl = 2;
while (nl >= 0){
cout << "l[" << nl << "] = ";
int pl = sizeof(unsigned long)*8-1;
while (pl>=0){
if ((((unsigned long)1 <<pl) & l[nl]) != 0){
cout << 1;
}
else {
cout << 0;
}
if (pl % 8 == 0){ cout << " ";}
pl--;
}
cout << "\n";
nl--;
}
return 0;
}
The value of each element in the array displays correctly.
sizeof(unsigned int)=4
i[0] = 0
i[1] = 1
i[2] = 2
i[3] = 4
i[4] = 8
i[5] = 16
sizeof(unsigned long)=8
l[0] = 4294967296
l[1] = 17179869186
l[2] = 68719476744
It is interesting to note the resulting values in the array of long elements.
This is because long is twice the size of int, meaning that two adjacent int values make a long.
If you think of this in terms of bitshift, this would be like saying l[0] = (((long)i[1])<<32) | ((long)i[0]).
This indicates that the lest significant value is stored in the lowest index - typical of little endian. The bitwise representation highlights this further.
Finally we see the value of the bits for each element (ordered highest to lowest):
i[5] = 00000000 00000000 00000000 00010000
i[4] = 00000000 00000000 00000000 00001000
i[3] = 00000000 00000000 00000000 00000100
i[2] = 00000000 00000000 00000000 00000010
i[1] = 00000000 00000000 00000000 00000001
i[0] = 00000000 00000000 00000000 00000000
l[2] = 00000000 00000000 00000000 00010000
00000000 00000000 00000000 00001000
l[1] = 00000000 00000000 00000000 00000100
00000000 00000000 00000000 00000010
l[0] = 00000000 00000000 00000000 00000001
00000000 00000000 00000000 00000000
Indeed we see that the least significant bit has the lowest address, and the least significant byte has the lowest address. This is what you would expect of little endian ordering. Maybe the code is running on an x86 processor, which is known to use little-endian.