Array rotation with Python

YouFolio is an online portfolio (e-portfolio) company working with students, universities and businesses to showcase skills and help talented individuals land their dream jobs by making their content search engine optimized and verifiable. As an early stage company, it has a strong focus on problem solving and therefore bases its interview questions on real-life YouFolio solutions. If an interviewee solves a problem more efficiently than YouFolio's current implementation, they are often invited to join the team. The larger companies are using Python for interviews, so we will too.

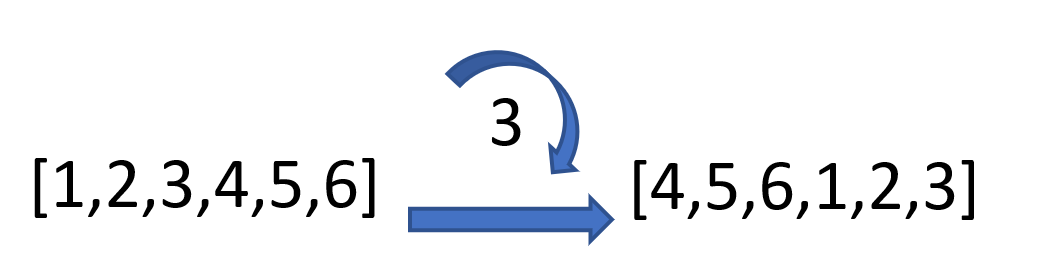
A frequently used data stream is the list of active account ids (assume a list of integers). This list gets returned very frequently and therefore is stored in memory, but it has one problem: people who signed up first get displayed first. As much as the YouFolio founders and early adopters love recognition, we want the users to get the most from the experience and therefore we need to rotate the array. We want to be able to rotate the array some arbitrary number (in this example, we'll rotate the array by 3 spaces). We tried using memory copying but the array is just too large.

Right now we can solve the problem O(n/c) time complexity using a smaller allocation, but we are happy with O(n) for a few reasons.

• The entire operation can be performed on the stack with no risk of stack overflow
• We would not be attempting an allocation that can't be done

def rotate(nums, k):
	"""
	:type nums: List[int]
	:type k: int
	:rtype: None Do not return anything, modify nums in-place
	"""      

The goal of this algorithm is to

• Create as few allocations as possible
• Only set each element once

Now let's implement this API.

#!/usr/bin/python2.7

def rotate_kn(nums, k):
	"""
	:type nums: List[int]
	:type k: int
	:rtype: None Do not return anything, modify nums in-place
	"""
	for x in range(0, k):
		le = nums[0]
		ri = le
		for y in range(1, len(nums)):
			ri = nums[y]
			nums[y] = le
			le = ri
		nums[0] = le

Well, that was the naive solution with O(k*N) complexity. Do we want to try for O(N) complexity?

	
def rotate_n(nums, k):
	"""
	:type nums: List[int]
	:type k: int
	:rtype: None Do not return anything, modify nums in-place
	"""
	# Get the length and make sure there is something to rotate
	l = len(nums)
	if l < 2:
		return
	
	# Make sure the rotation is within the length
	k = k % l
	if (k == 0):
		return
	
	init = 0
	count = 0
	o = nums[init]
	i = k + init
	r = o
	while init < k and count < l:
		while (i != init):                
			r = nums[i]
			nums[i] = o
			i = (i + k) % l
			o = r
			count += 1
			
		nums[init] = o
		init = init + 1
		o = nums[init]
		i = k + init
		count += 1
			

It's not exactly intuitive given the nested while loops, but when you consider the stride and the break criteria, it works out to be O(N).

Time to invoke the code...

arr = [1,2,3,4,5,6,7,8,9,10]
print("The original array is:")
print(arr)
print("")
rotate_kn(arr, 3)
print("Rotated with 3N complexity:")
print(arr)

arr = [1,2,3,4,5,6,7,8,9,10]
rotate_n(arr, 3)
print("Rotated with N complexity:")
print(arr)
print("")
print("If both answers match, it's right")
print("")

Now let's see the output...

The original array is:
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

Rotated with 3N complexity:
[8, 9, 10, 1, 2, 3, 4, 5, 6, 7]
Rotated with N complexity:
[8, 9, 10, 1, 2, 3, 4, 5, 6, 7]

Success! This traverses the collection in O(n) complexity (one node for each element) and O(5) space complexity (5 stack allocations). This is fine for this collection... In other words, this can handle future growth.

Want to try for a more efficient algorithm? Here's a link to get started.