YouFolio is an online portfolio (e-portfolio) company working with universities and students to showcase their skills and help them land their dream jobs by making their content search engine optimized and verifiable. As an early stage company, it has a strong focus on problem solving and therefore bases its interview questions on real-life YouFolio solutions. If an interviewee solves a problem more efficiently than YouFolio's current implementation, they are often invited to join the team.
YouFolio gets new users each year from a University. So far, every university we have worked with gives each user/perspective student a unique integer ID. These IDs increment such that we know what year a student was supposed to start at a university based on their ID and the high and low value of that year's IDs (a cohort).
For most universities, this data is sparse because not all perspective students attend or complete the program at that university or college. The accounts of non-students are not provided to YouFolio. As you may know, YouFolio has a server for each university. Since this data structure is so common, we have similarily sharded each university data by cohort. Account information for each university is stored in a hash map, with each entry an ordered array for the cohort.
Given we know the year of a student, the goal is to efficiently acquire their account information based on their user ID. There are many approaches to solve this problem, but consider time and space complexity.
While a tree might be an efficient way to find a value, you do have to build the tree - taking both time and memory.
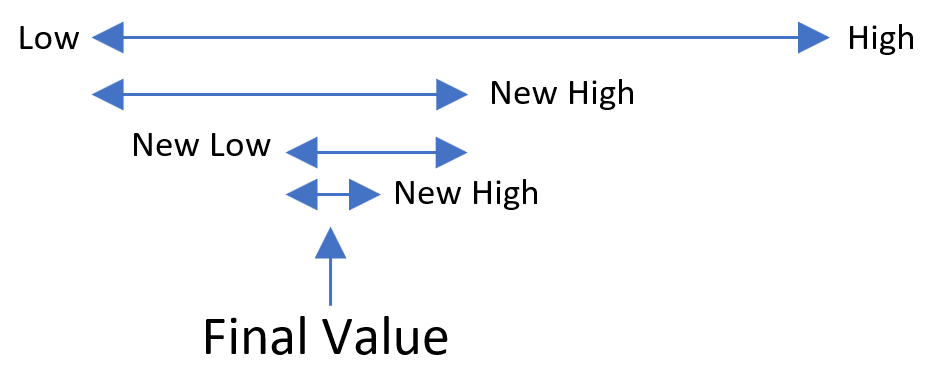
Really, with an ordered array, you can find an falue in O(log n) time using interval halving, which has no space complexity because you are using the data without creating any type of supporting structure.
Because all the big tech companies make you interview in Python, so does YouFolio:
#!/usr/bin/python2.7
from random import randint
class Interval:
item_of_interest = 0
left = 0
right = 0
def __init__(self, left: int, item_of_interest: int, right: int):
"constructor to initiate an interval"
# store data
self.left = left
self.item_of_interest = item_of_interest
self.right = right
return
def __str__(self):
"allows you to call print() on an interval"
return "[" + str(self.left) + "|" + str(self.item_of_interest) + "|" + str(self.right) + "]"
def mid_range(self) -> int:
"gets the middle of a range (good for making next guess)"
return int((self.right - self.left)/2 + self.left)
def item_of_interest_or_higher(self, val: int) -> bool:
"determines if guess is higher than the item of interest"
return val >= self.item_of_interest
def clone(self):
return Interval(self.left, self.item_of_interest, self.right)
@classmethod
def make(self, left: int, right: int):
"makes a random interval"
item_of_interest = randint(left+1, right-1)
if right < left:
item_of_interest = randint(right+1, left-1)
return Interval(left, item_of_interest, right)
@classmethod
def halv(self, data) -> int:
"uses interval halving methods to find the median"
if abs(data.right - data.left)<2 :
return data.right
mid = data.mid_range()
if data.item_of_interest_or_higher(mid):
data.right = mid
else:
data.left = mid
return Interval.halv(data)
Now let's invoke the code...
c = Interval.make(1,1000)
print("the interval we created for this example is " + c.__str__())
print("the item the interval halving algorithm found is " + str(Interval.halv(c.clone())))
If correct, we should be able to find the item of interest using interval halving.
the interval we created for this example is [1|416|1000] the item the interval halving algorithm found is 416
Success! Want to try for a more efficient algorithm? Here's a link to get started.