Building a Mentorship Tree from a Sorted Array

YouFolio is an online portfolio (e-portfolio) company working with universities and students to showcase their skills and help them land their dream jobs by making their content search engine optimized and verifiable. As an early stage company, it has a strong focus on problem solving and therefore bases its interview questions on real-life YouFolio solutions. If an interviewee solves a problem more efficiently than YouFolio's current implementation, they are often invited to join the team.

YouFolio has scored (low score is better) and ordered its users who have elected to participate in the mentorship program. The mentorship score is based on how well a user's profile ranks in Google (essentially it is based on SEO - think, "getting on the n-th page of Google" - low score is best). This program allows for individuals to help two other YouFolio users improve the quality of their portfolios - thus helping them get recognized as the experts they are. As a goal, each user gets one mentor, and two mentees. We also want this match to be somewhat close in score. For example, 1 should mentor 2 and 3.

We find this approach works well as active user engagement is better than passive. Of course, you may now be saying "won't half the users have no mentees?" and you are correct. We have found that everyone takes the mentor's role more seriously when there is some exclusivity.

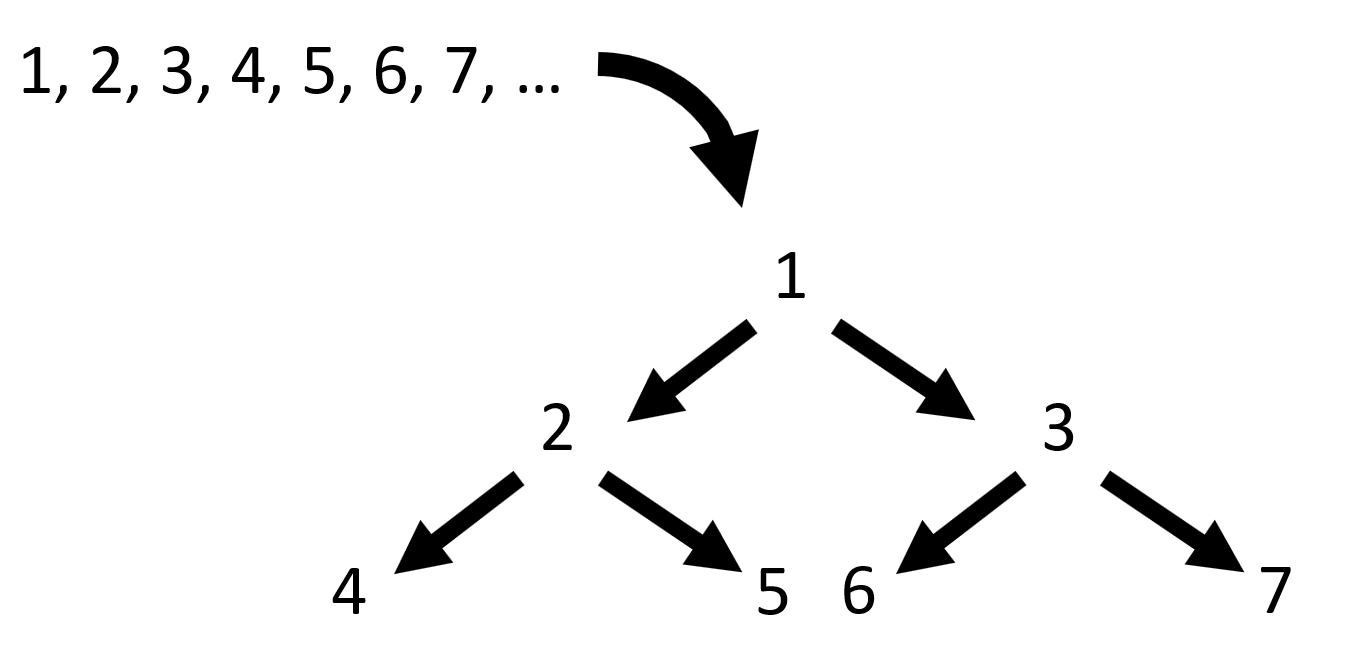
So here is the challenge: given an ordered collection, create a tree with the lowest scores at the top. For a given level in a tree, the lowest score is at the left.

Here is the API we currently use. In the make method, the only required parameters are the implicit self and data - the rest are optional! This API is in Python because all the big tech companies conduct their interviews in Python.

class Node: 
    
    data : int 		#the user's ID
    left = None
    right = None

 @classmethod
    def make(self, data: [int], ...):
        "constructor to initiate nodes"
	
	def get_size(self) -> int:
        "gets the size of the tree" 
            

The goal is to implement this API in a manner that balances insert penalty and read speed. There are some efficiencies that can be gained by using addition over multiplication if possible. Also passing variables instead of re-calculating them may help.

Now let's implement this API.

#!/usr/bin/python2.7

class Node:
    "the basic element of a tree"
    
    data = -1
    left = None
    right = None
        
    def __init__(self, data: int):
        "constructor to initiate a node"
        
        # store data
        self.data = data
        
        # store reference (next item)
        self.left = None
        self.right = None
        return

    @classmethod
    def make(self, data: [int], index : int = 0, level_size : int = 1, prev_sum: int = 0):
        "constructor to initiate nodes"
        if index >= len(data):
            return None
        
        # the data to be returned
        ret = Node(data[index])
        
        # note: level_size should be 2^level, so either level or level_size can be passed
        #       but passing a variable means you don't have to calculate it 2x, so it's a bit faster
        child_index = index + level_size # the next index will be the current index + level_size
        child_index += (index - prev_sum) # plus how ever far the index passed the last level's sum
        # child_index = index * 2 + 1 # the expected index for the non-sparse case
        current_sum = prev_sum + level_size # the total number of elements reviewed
        next_level_size = level_size + level_size # the expected size of the next level
            
        ret.left = Node.make(data, child_index, next_level_size, current_sum)
        ret.right = Node.make(data, child_index+1, next_level_size, current_sum)            

        return ret

    def serialize(self) -> str:
        "will turn the entire tree into a single line string"
        s = ""
        s += str(self.data)
        if self.left != None or self.right != None:
            s += " ["
            if self.left != None:
                s += self.left.serialize()
            else:
                s += "null"
            s += " "
            if self.right != None:
                s += self.right.serialize()
            else:
                s += "null"
            s += "]"
        return s

    def __str__(self, level=0):
        "allows you to call print() on a node"
        return self.serialize()

	def get_size(self) -> int:
        "gets the size of the tree"
        s = 1
        if self.left != None:
            s += self.left.get_size()
        if self.right != None:
            s += self.right.get_size()
        return s  

Time to invoke the code...

vals = list(range(1,31+1))
c = Node.make(vals)
print("The size is ", c.get_size())
print("The value is ", c.serialize())
print(c)

Now let's see the output...

The size is 31
The value is  1 [2 [4 [8 [16 17] 9 [18 19]] 5 [10 [20 21] 11 [22 23]]] 3 [6 [12 [24 25] 13 [26 27]] 7 [14 [28 29] 15 [30 31]]]]

Success! This traverses the collection in O(n) complexity and successfully builds a tree of O(n) space complexity (one node for each element).

Want to try for a more efficient algorithm? Here's a link to get started.