The FLP theorem highlights the fundamental challenges in distributed systems and has had a profound impact on the design and reason about these systems. While it proves that perfect consensus is impossible under certain conditions, it has also spurred the development of practical solutions that work well in real-world scenarios.
Understanding the FLP theorem and its implications is crucial for anyone working with distributed systems.
What is Consensus?
Consensus in distributed systems refers to the ability of multiple distributed processes to reach an agreement on something. This could be:
- The value of a piece of shared state
- A decision to take a particular action
- The current timestamp to associate with an action
- Reaching a specific point in execution
A common example of consensus is in distributed database transactions. Imagine transferring funds between two bank accounts, each stored on a different server. Both servers must agree on whether the transaction succeeds or fails to ensure the accounts are correctly updated.
The Challenges of Reaching Consensus
Several factors make consensus difficult in distributed systems:
- Non-determinism: Multiple operations can occur simultaneously, and their order may vary across different executions.
- Lack of global time: There is no universal clock that all nodes can reference.
- Unreliable networks: Communication between nodes can be unpredictable or fail.
- Faulty or malicious nodes: Some nodes may crash, behave erroneously, or intentionally try to disrupt the system.
Properties of Consensus
A robust consensus protocol should guarantee three key properties:
- Termination (Liveness): All non-faulty processes eventually decide on a value.
- Agreement: All processes decide on the same value.
- Validity: The decided value must have been proposed by one of the processes.
The FLP Theorem: A Fundamental Impossibility Result
In 1985, Michael Fischer, Nancy Lynch, and Michael Paterson published a groundbreaking paper titled "Impossibility of Distributed Consensus with One Faulty Process." This work, which later won the Dijkstra Award, introduced what is now known as the FLP theorem.
The FLP theorem states that in an asynchronous distributed system where even one process might fail, it is impossible to guarantee that a consensus algorithm will always terminate. This result holds even under a very simple failure model (fail-stop) and with minimal assumptions about the system.
The System Model
The FLP theorem considers a distributed system with the following characteristics:
- Asynchronous communication: Messages may be delayed or reordered but not corrupted.
- At most one faulty processor.
- Fail-stop failure model: A faulty process simply stops working.
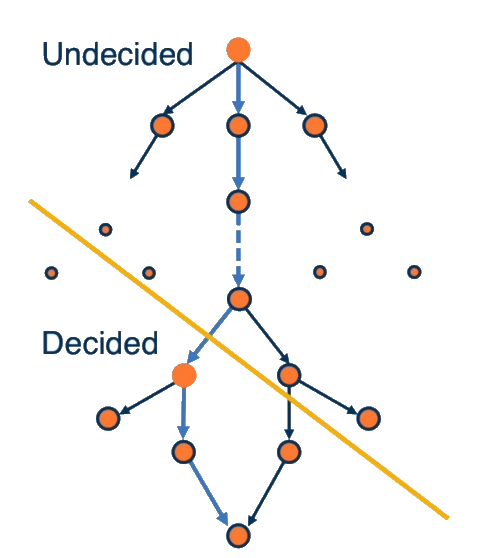
The Proof (Simplified)
The proof of the FLP theorem is complex, but the core ideas can be summarized as follows:
- There must be some initial configuration where the final result is not predetermined.
- There must be a single event (like a message) that changes the system from an undecided state to a decided state.
- It is possible for this crucial message to be delayed indefinitely, preventing the system from ever reaching a decision.
Implications and Practical Solutions
The FLP theorem might seem to suggest that building reliable distributed systems is impossible. In practice, various consensus protocols like Two-Phase Commit, Paxos, and Raft are used to build effective distributed systems.
These protocols work around the FLP impossibility result by relaxing some of the assumptions or accepting weaker guarantees. For example:
- Using timeouts to detect failures (which introduces a degree of synchrony).
- Accepting that consensus might not be reached in some rare cases.
- Using randomization to break symmetry and help the system progress.
Key Concepts
Distributed Systems A collection of independent computers that appear to users as a single coherent system. These computers (or nodes) communicate and coordinate their actions by passing messages to one another over a network.
Consensus The ability of multiple distributed processes to reach an agreement on a single data value, action, or state. This is crucial for maintaining consistency across a distributed system.
Node An individual computer or process within a distributed system that can perform computations and communicate with other nodes.
Asynchronous System A system where there are no timing assumptions. Messages may be delayed arbitrarily, and there is no global clock. Processes may execute at different speeds.
Synchronous System A system where there are known bounds on message transmission delays and process execution speeds. This is in contrast to an asynchronous system.
Fault Tolerance The ability of a system to continue operating correctly even when some of its components fail.
Fail-Stop Failure A type of failure where a faulty process simply stops executing and remains silent. This is considered one of the simplest failure models.
Liveness A property of a distributed system that guarantees progress will eventually be made. In the context of consensus, it means that all non-faulty processes will eventually decide on a value.
Safety A property that ensures nothing bad ever happens in the system. In consensus, it means that all processes that decide must decide on the same value.
FLP Theorem Named after Fischer, Lynch, and Paterson, this theorem proves that in an asynchronous system with even one faulty process, no consensus protocol can guarantee both safety and liveness.
Bivalent Configuration A state of the system where the final decision is not yet determined, and multiple outcomes are still possible.
Univalent Configuration A state of the system where the final decision is already determined, even if not all processes have reached it yet.
Two-Phase Commit (2PC) A distributed algorithm for coordinating all the processes that participate in a distributed atomic transaction on whether to commit or abort the transaction.
Paxos A family of protocols for solving consensus in a network of unreliable processors. Paxos is one of the most widely used consensus algorithms in distributed systems.
Raft A consensus algorithm designed as an alternative to Paxos. It was designed to be more understandable than Paxos while also providing a foundation for building practical systems.
Byzantine Fault Tolerance The ability of a system to continue operating correctly even when some nodes fail in arbitrary ways, including becoming malicious. This is a more general (and difficult) problem than simple crash failures.
Eventual Consistency A consistency model used in distributed computing to achieve high availability. It informally guarantees that, if no new updates are made to a given data item, eventually all accesses to that item will return the last updated value.
Quorum The minimum number of votes that a distributed transaction has to obtain in order to be allowed to perform an operation in a distributed system.
Partition Tolerance The ability of a distributed system to continue functioning despite arbitrary message loss or failure of part of the system.
CAP Theorem States that it is impossible for a distributed data store to simultaneously provide more than two out of the following three guarantees: Consistency, Availability, and Partition tolerance.
Review Questions
What is consensus?
Consensus in distributed systems refers to the ability of multiple distributed processes to reach an agreement on something. This could be:
- Agreeing on the value of a shared piece of state
- Agreeing to take a particular action
- Agreeing on a timestamp for an action
- Agreeing on reaching a certain point in execution
Explain in your own words/understand all elements of the definition in the papers/video
A key example is agreeing on the outcome of a transaction across multiple servers, like in a banking system. Consensus is critical for ensuring distributed systems behave correctly and consistently.
The transcript outlines three key properties for consensus:
- All non-faulty processes eventually decide on a value (termination/liveness)
- All processes decide on the same single value (agreement)
- he agreed value must have been proposed by one of the processes (validity)
What is the goal of the FLP work, what did they want to learn/prove?
The goal of the FLP (Fisher, Lynch, Patterson) work was to determine if it is possible to guarantee that consensus can always be reached in a distributed system under certain conditions. Specifically, they wanted to prove whether consensus is possible in an asynchronous system with at most one faulty processor using a fail-stop failure model.
Provide intuition about the approach they took to achieve this goal.
Their approach was to analyze a simplified system model and try to identify if there could be any starting configuration and legitimate run of the system that would not reach a deciding state. In other words, they attempted to find at least one scenario where consensus could not be guaranteed.
State the FLP theorem and provide intuition of the proof/do you understand it?
The FLP theorem states: In a system with one faulty process, no consensus protocol can be totally correct.
The intuition of the proof is as follows:
- They start with a system where nodes can decide on either 0 or 1.
- They prove that there must be some initial configuration where the final result is not predetermined.
- They argue that there must be a single event (like a message) that changes the system from an undecided (bivalent) state to a decided (univalent) state.
- Finally, they show it is possible for this crucial message to be sufficiently delayed, preventing the system from transitioning to a decided state.
This means there will always be a possible scenario (an admissible run) where consensus is not reached, thus proving it is impossible to guarantee consensus in all cases under these conditions.
What is the intuition about the significance of FLP, in light of much other work of consensus algorithms, replication protocols, …
The FLP result is significant because it proves a fundamental limitation in distributed systems. It shows that under very general assumptions (asynchronous communication, possibility of one fault), we cannot guarantee that consensus will always be reached.
However, this does not mean that practical consensus algorithms are impossible. Rather, it means that practical consensus protocols must relax some of the assumptions or accept that consensus might not always be reached under certain conditions.
Real-world consensus protocols like Two-Phase Commit, Paxos, or Raft work around this limitation by changing some of the initial assumptions or by specifying the conditions under which they will or will not terminate or reach consensus. This allows us to build reliable distributed systems, but with the understanding that there may be extreme scenarios where consensus cannot be guaranteed.
The FLP result thus provides a crucial theoretical foundation for understanding the challenges and limitations in distributed systems, guiding the development of practical consensus algorithms that work within these constraints.