engineering

Selling the idea of Code Coverage to a Customer

Posted in engineering by Christopher R. Wirz on Wed Apr 01 2020

Code coverage is best practice and a worthy investment - but how do you convince the customer?

TCP rewrite to modify packet captures

Posted in engineering by Christopher R. Wirz on Wed May 02 2018

TCP rewrite can be used to modify packet captures - allowing you to replay traffic to different ports and addresses.

Timeout detection and recovery (TDR) settings to support AI/ML in Windows

Posted in engineering by Christopher R. Wirz on Mon May 08 2017

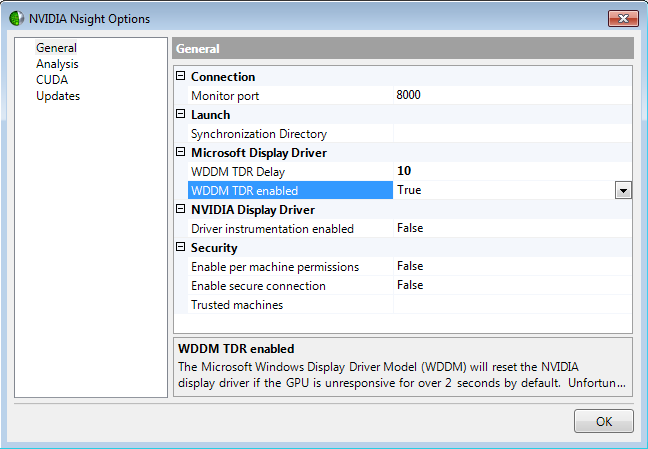
One of the most common stability problems in AI/ML training occurs when a computer hangs, or when it appears to be completely frozen while, in reality it is still training.

Set Theory Symbols

Posted in engineering by Christopher R. Wirz on Wed Feb 08 2017

Set notation is an important convention in computer science. This cheat sheet is extremely useful.

Air Data Calculations

Posted in engineering by Christopher R. Wirz on Sat Jun 11 2011

Calculate ISA values for standard day in browser using javascript. Standard day calculations are based on the air column theory to determine atmospheric conditions at a given altitude.

Feed Forward Gradient Descent using Matrix Math

Posted in engineering by Christopher R. Wirz on Wed Jun 18 2008

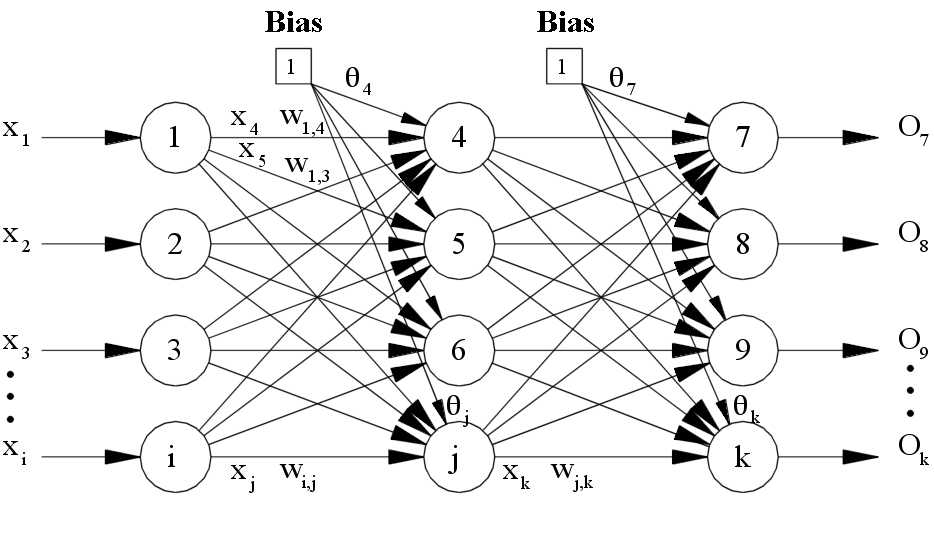
Feed forward neural networks can be represented by matrix math and can use analytical gradient descent.

Weighted Least Squares and the Pseudo-Inverse

Posted in engineering by Christopher R. Wirz on Mon May 19 2008

While least squares does not give precedence to the error on certain measurements, the weighted least squares can.

Least Squares and the Pseudo-Inverse

Posted in engineering by Christopher R. Wirz on Sun May 18 2008

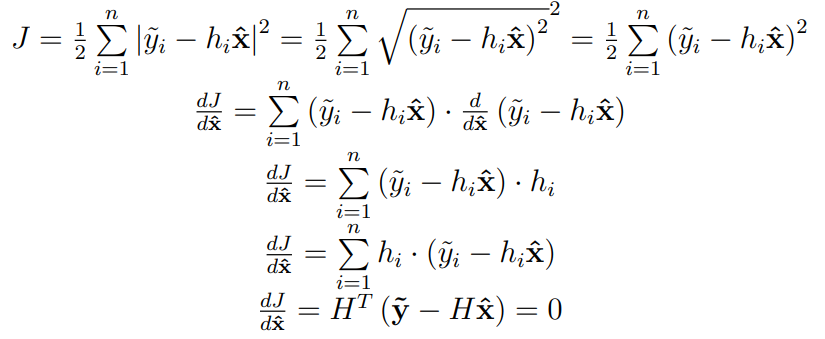
The least squares problem has an analytical solution - achieving a feasible solution when minimized.

Orthogonal Basis Functions in Matlab

Posted in engineering by Christopher R. Wirz on Tue Apr 08 2008

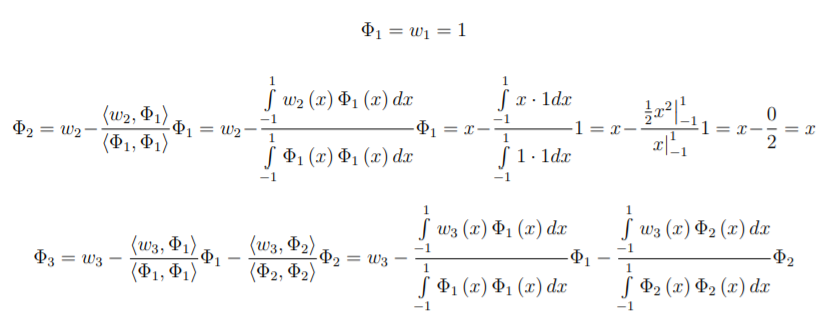
Gram-Schmidt orthogonalization takes a nonorthogonal set of linearly independent functions and constructs an orthogonal basis over an arbitrary interval